
Incorrect. This graph correctly represents a function and its inverse. Notice that the two lines reflect over y=x.
The formula C = five-ninths 5 9 (F − 32) gives the degrees Celsius as a function of the degrees Fahrenheit. You would like to convert 16° Celsius to Fahrenheit using the inverse of the function C = five-ninths 5 9 (F – 32). Find the inverse of the function and the degrees Celsius.
A. F = five-ninths 5 9 (C – 32), -8.89° F
Incorrect. Find the inverse of the function by solving for F.
B. F = five-ninths 5 9 (C + 32), 40.89° F
Incorrect. Find the inverse of the function by solving for F.
C. F = nine-fifths 9 5 (C + 32), 60.8° F
Correct!
D. F = nine-fifths 9 5 (C + 32), 86.4° F
Incorrect. Find the inverse on the function by solving for F.
Which of the following does NOT represent a function and its inverse?
A.
| X | -2 | 0 | 4 |
| Y | 3 | -2 | -8 |
| X | -8 | -2 | 3 |
| Y | 4 | 0 | -2 |
B.

Incorrect. This graph correctly represents a function and its inverse. Notice that the two lines reflect over y=x.
C.
f(x) = 3x + 6
f -1(x) = one-third 1 3 x − 2
Incorrect. These equations do represent a function and its inverse. You can check by substituting 3x + 6 in for x of the inverse and see if you get x.
D.
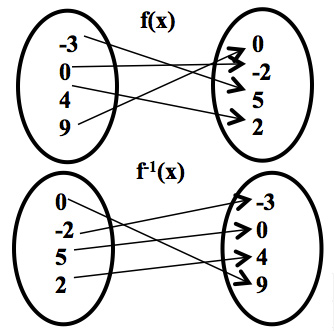
Correct! These mapping diagrams do NOT represent a function and its inverse. Remember that an inverse function interchanges the input and output values.
Maria is making tacos for a friend’s birthday party. She decided it would be easier to make a table showing the number of tacos needed depending on the number of people attending. Below is the table Maria created.
|
People
|
Tacos
|
|
2
|
5
|
|
5
|
12
|
|
8
|
20
|
|
12
|
32
|
|
15
|
40
|
The host wasn’t sure how many people to invite, so Maria showed her the inverse of the table she created. Determine the inverse of this table.
A.
|
Tacos
|
People
|
|
2
|
5
|
|
5
|
12
|
|
8
|
20
|
|
12
|
32
|
|
15
|
40
|
B.
|
Tacos
|
People
|
|
40
|
15
|
|
32
|
12
|
|
20
|
8
|
|
12
|
5
|
|
5
|
5
|
C.
|
Tacos
|
People
|
|
40
|
2
|
|
32
|
5
|
|
20
|
8
|
|
12
|
12
|
|
5
|
15
|
D.
|
Tacos
|
People
|
|
2
|
40
|
|
5
|
32
|
|
8
|
20
|
|
12
|
12
|
|
15
|
5
|
Which of the following graphs correctly shows a function and its inverse?
A.
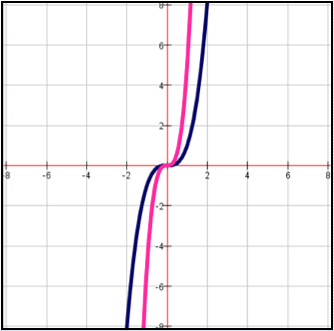
Incorrect.The graphs do not reflect over y=x.
B.
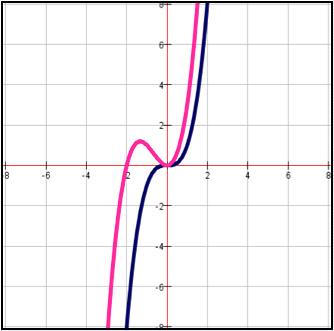
Incorrect.The graphs do not reflect over y=x.
C.
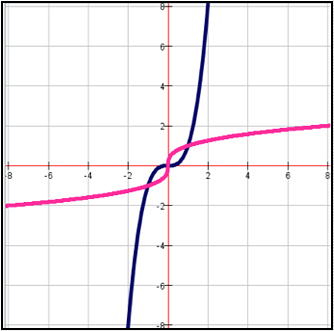
Correct! The graphs reflect over y = x.
D.
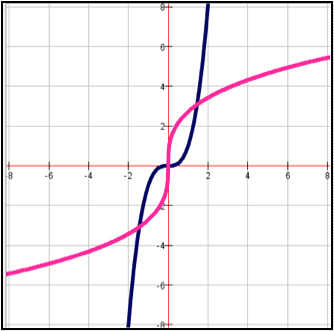
Incorrect.While it’s close, the graphs do not reflect over y = x.
Saul was practicing finding the inverse of functions several different ways. Once he found the inverse of the function, he was trying to decide which inverse was a function or an inverse function. Select the function that has an inverse function or a one-to-one correspondence.
A.
|
x
|
y
|
|
-2
|
3
|
|
0
|
-4
|
|
1
|
3
|
|
2
|
0
|
|
3
|
2
|
B. f(x) = 2x2 – 3.5
Incorrect. The inverse of the function is  which is not a function; you can sketch it and use the vertical line test to double check.
which is not a function; you can sketch it and use the vertical line test to double check.
C.
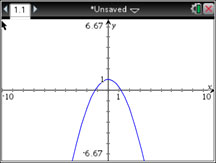
Incorrect. Sketch the inverse of the function reflecting over the line y = x and then use the vertical line test to see if the inverse is a function.
D.
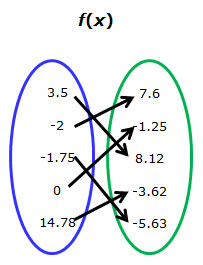
Correct!